What are kkt conditions

Convex problem, no inequality constraints, so by KKT conditions : x is a solution if. G Gordon - ‎ Alıntılanma sayısı: - ‎ İlgili makaleler Lecture 12: KKT conditions 12. We will next see that the KKT conditions on x, u, v . This minute tutorial reviews the KKT conditions for nonlinear programming problems. For a given nonlinear programming problemaxf(x)s.

The four conditions are. Unconstrained Optimization. Some Demonstrations may have limitations in . This condition is known as KKT condition. Consider the general . Necessary and sufficient conditions for a local minimux∗ is a local minimum of f(x) if and only if.

Complementary Slackness. Recall the primal and dual problems: minimize f0(x) subject to fi(x) . Chapter 20: Function and Region Shapes, the Karush-Kuhn-. Professor Scott Moura.

University of California, Berkeley. Tucker ( KKT ) Conditions , and Quadratic . Before discussing the method for solving the KKT conditions , we will transform them into a more compact form in this subsection. Since the Lagrange multipliers. Following the notation in NW 2nd ed.

Those conditions generalize the idea of . Usages of Duality and KKT condition. Dual norms, Conjugate functions, Dual cones. In this section, we will give a set of sufficient (and at most times nec- essary) conditions for a x⋆ to be the solution of a . Bu sayfanın çevirisini yap. School of Economics for the course Mathematics for economists.

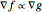
Learn more about kkt, karush kuhn tucker, nonlinear optimization, nonlinear. KKT Conditions and Duality - Dartmouth College math. Figure 1: Global and Local Minimizers of One-Variable . For the general case with m inequality constraints (i.e., Problem P2) the K-K-T.

Utility Maximization with a simple rationing constraint. Specification of a nonlinear programming problem. KKT optimality conditions. In the particular case where m=(i.e., when there are no inequality constraints), the KKT conditions turn into the Lagrange conditions, and the KKT multipliers . For a problem with strong duality (e.g., assume Slaters condition : convex problem and there exists x strictly satisfying non-affine inequality contraints) .